Sphärische Linsen: ein Leitfaden

Sphärische Linsen sind optische Linsen mit einer oder zwei Oberflächen, die wie ein Sphäre geformt sind, d. h. diese Oberflächen können durch einen zentralen Referenzpunkt und einen fixen Krümmungsradius definiert werden. sphärische Linsen sind die häufigste Form optischer Linsen, da sie einfach zu entwerfen und herzustellen sind und sich die Qualität leicht überprüfen lässt. Im folgenden Leitfaden erfahren Sie mehr über sphärische Linsen, ihre Verwendung und Herstellung.

Wofür werden Sphärische Linsen genutzt?

Sphärische Linsen werden in Anwendungen eingesetzt, bei denen Licht konvergiert oder divergiert wird, um ein kleineres oder größeres Bild eines Objekts/Sichtfelds zu erzeugen.

Bei einer Kamera beispielsweise werden Linsen verwendet, um das Bild eines nahen oder fernen Objekts auf einen Sensor (oft einen CMOS-Sensor) von mehreren mm Breite zu fokussieren. Wenn Sie ein Gebäude fotografieren, wird dieses Bild in exakten Proportionen von mehreren Metern auf einige mm verkleinert und in digitale Informationen umgewandelt, damit Sie es ausdrucken können.

Umgekehrt vergrößert das Objektiv eines Mikroskops ein sehr kleines Objekt auf ein breiteres Bild, das entweder mit dem bloßen Auge auf einem Okular oder mit einem digitalen Sensor betrachtet werden kann.

Arten von Sphärischen Linsen

Sphärische Linsen werden normalerweise durch die Form ihrer beiden Oberflächen definiert, die entweder flach, konkav oder konvex sind.

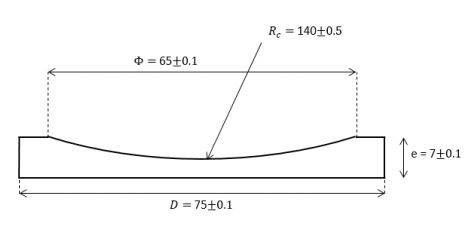
Abbildung 1: eine Plano-Konkave Linse mit einer ebenen Fläche und einer sphärischen, konkaven Fläche (mit einem Krümmungsradius von 140 mm in diesem Beispiel).

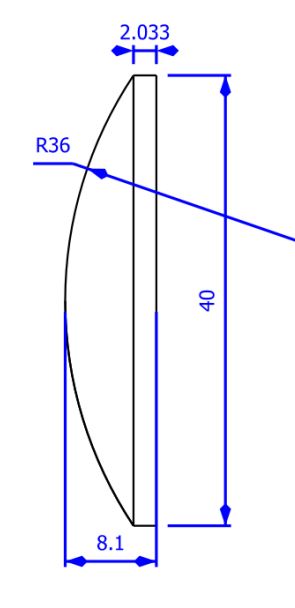
Abbildung 2: eine Plano-Konvexe Linse mit einer ebenen Fläche auf der rechten Seite und einer sphärischen, konvexen Fläche auf der linken Seite mit einem Krümmungsradius von 36 mm in diesem Beispiel.

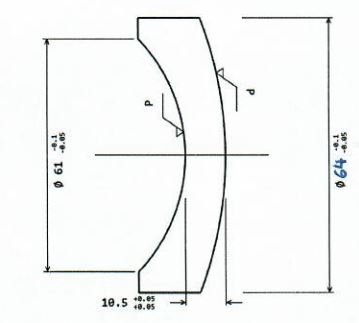
Abbildung 3: Meniskuslinse. Linse mit einer sphärischen, konkaven Oberfläche auf der linken Seite und einer sphärischen, konvexen Oberfläche auf der rechten Seite.

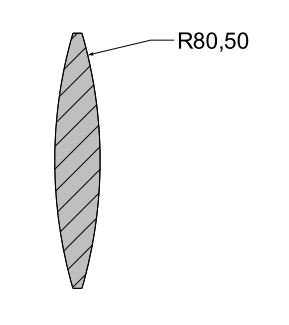
Abbildung 4: eine bikonvexe Linse mit zwei sphärisch, konvexen Flächen mit einem Krümmungsradius von 80,5 mm für beide Seiten in diesem Beispiel.

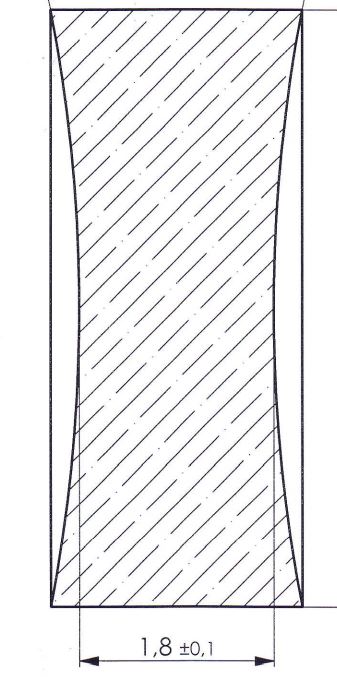
Abbildung 5: eine bikonkave Linse mit zwei sphärischen, konkaven Flächen und einer mittleren Dicke von 1,8 mm in diesem Beispiel.

Bemerkungen:

• Es gibt auch Linsen, bei denen eine Seite nicht sphärisch und die andere Seite sphärisch ist.
• In einigen Veröffentlichungen wird ein optisches Element, bei dem beide Flächen flach sind, als „flache Linse“ bezeichnet. Die Bezeichnung optisches Fenster ist jedoch passender, da sie nicht so geformt sind, dass sie das Licht konvergieren oder divergieren.

Wie werden Sphärische Linsen hergestellt?

Standardmäßige Schritte der Herstellung von sphärischen Linsen sind folgende:

1. Zuschnitt oder Guss des Rohlings der Linse

2. Abschleifen des Teils, bis zur richtige Form.

3. Polieren beider optischer Flächen auf einer halbautomatischen Poliervorrichtung

4. Zentrierung / Einfassung des Objektivs, um die mechanische Achse des Objektivs mit der optischen Achse in Einklang zu bringen. Die Zentrierung des Objektivs ist sehr wichtig, da eine schlechte Zentrierung zu einer Verschlechterung der optischen Eigenschaften des optischen Systems nach der Montage führt.

5. Reinigung der Linse mit Ultraschallreinigungsgeräten.

6. Beschichtung der Linse

Welche Materialien für die Herstellung von Sphärischen Linsen?

Die meisten optischen Materialien können zur Herstellung einer sphärischen Linse verwendet werden, wobei die Wahl des Materials nach folgenden Kriterien erfolgen sollte:

• Brechungsindex (definiert, wie die Lichtstrahlen an der Grenzfläche zwischen Luft und Material reagieren)
• Abbe-Zahl (definiert die chromatische Dispersion)
• genutzte Wellenlänge (UV, sichtbar, IR)
• Schmelzungspunkt, falls die Linse per Spritzguss gefertigt werden soll
• Verfügbarkeit / Kosten des Materials. Materialien können zwar von den Eigenschaften her perfekt zu Ihrem Projekt passen, sind aber möglicherweise nicht verfügbar oder sehr teuer, weshalb ein ähnliches Material in Betracht gezogen werden kann.
• Einsatzbedingungen: für extreme Bedingungen kann z. B. ein besonders hartes Material wie Saphir gewählt werden.

Wenn es keine besonderen Einschränkungen gibt, empfehlen wir die Verwendung von optischem Glas N-BK7 (Schott) / HK9L (CDGM), das weithin verfügbar und relativ preiswert ist.

Wie viel kostet eine Sphärische Linse?

Linsen gibt es in verschiedene Preisklassen. Die entscheidenden Faktoren sind in der folgenden Liste dargestellt.

PARAMETER	EINFLUSS AUF PREIS DER LINSE
Rohmaterial	Standard-Materialien: N-BK7/HK9L/B270/ Quarzglas/Kunststoff, bis hin zu teureren Materialien: Saphir, Germanium, Silizium, sehr spezielle optische Materialien
Größe	Sehr kleine (weniger als 5 mm) und besonders große Objektive (mehr als 100 mm) sind aufgrund der mit der Größe verbundenen Polierprobleme teurer in der Herstellung.
Optische Spezifikationen	Polierqualität und Oberflächengüte haben einen sehr großen Einfluss auf den Preis einer sphärischen Linse
Bestellmenge	Das Polieren von sphärischen Linsen kann in parallelen halbautomatischen Poliermaschinen erfolgen, was bedeutet, dass für die Herstellung von einem oder zehn Teilen fast die gleiche Zeit und die gleichen Ressourcen benötigt werden.
Optische Beschichtung	Optische Beschichtungen werden pro Charge durchgeführt. Eine Charge kostet in der Regel mehrere Hundert USD. Je mehr Teile gleich beschichtet werden, desto günstiger wird der Stückpreis.

Brennweite Sphärischer Linsen

Der Brennpunkt einer sphärischen Linse ist der Punkt auf der optischen Achse, in dem ein einfallendes Bündel von Lichtstrahlen konvergiert und gebündelt wird.

Die Brennweite ist der Abstand zwischen dem Mittelpunkt der Linse und dem Brennpunkt. Die Brennweite ist ein positiver Wert, wenn es sich um eine Sammellinse handelt, und ein negativer Wert, wenn es sich um eine Zerstreuungslinse handelt.

Je nach der Form der Oberflächen kann eine sphärische Linse divergierend oder konvergierend sein.

Die Brennweitenformel (Gaußsche Formel) lautet:

1/u + 1/v = 1/f

Wobei :

u: Abstand des Objekts zum Mittelpunkt der Linse

v: ist der Abstand des Bildes vom Mittelpunkt des Objektivs

f: ist die Brennweite.

Bei einem Objekt im Unendlichen haben wir beispielsweise 1/u, das gegen 0 tendiert, also 1/v=1/f, also v=f, das Bild entsteht bei der Brennweite.

Eine sphärische Linse ist durch ihre optische Brechkraft definiert, die umgekehrt äquivalent zur Brennweite ist, d. h. je näher der Brennpunkt an der Linse liegt, desto größer ist die Brechkraft der Länge.

P=1/f

Dabei ist P die Brechkraft der Linse und f die Brennweite.

Die Simulation der Brennweite einer sphärischen Linse kann auf der Grundlage des Brechungsindex des Materials (Snell-Gesetz), der Dicke der Linse und des Krümmungsradius durchgeführt werden. Da die Berechnung etwas kompliziert ist, raten wir Nutzern sphärischer Linsen, eine Simulationssoftware (wie Zemax) zu verwenden, um einen zuverlässigen Wert zu erhalten.

Konzentrizität Sphärischer Linsen

Die optische Konzentrizität ist eine Schlüsselfaktor. Optische Linsen haben in der Regel zwei Arten von Toleranzen.

1. Die optische Toleranz
2. Die mechanische Toleranz

Die Konzentrizität ist eine direkte Verbindung zwischen beiden. Die Konzentrizität des Objektivs bestimmt, wie nahe der optische Mittelpunkt am mechanischen Mittelpunkt liegt. Dies ist besonders wichtig bei einem optischen System, bei dem mehrere Objektive eingebaut sind, da sich die Konzentrizitätsfehler der einzelnen Objektive addieren können.