Spherical lens for optics : a complete guide
Spherical lens refers to a type of optical lens with one or two surface shaped like a cut of sphere, meaning this surface can be defined from a center reference point and a fix radius of curvature. Spherical lens are the more commons form of optical lens, being easier to design, easier to manufacture and easier to check the quality. Learn more about spherical lens how they are used and manufacture in below guide.
What are spherical lenses used for?
Spherical lens are used in applications where light will be converged or diverged to form a smaller or bigger image of an object / field of view.
For example on a camera, lenses are used to focus the image of an object which is close or far from the device on a sensor (often a CMOS) of several mm wide. If you are taking a picture of a building, this building image will be shrink at exact proportions from several meters to several mm and transcribe into digital information so you would be ablet to print it.
On the opposite on a microscope the lens will enlarge a very small object to a wider image that can be seen either by raw eye on a eye piece or by a digital sensor.
What are the types of spherical lenses?
Spherical lenses are usually defined by the shape of their two surfaces, which is mix of flat, concave, and convex.
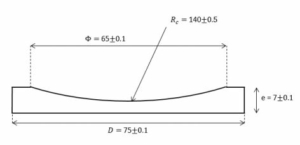
Illustration 1 : PCV lens
Illustration 1 : a Plano-concave lens (PCV lens), with a flat surface and a spherical concave surface (with radius of curvature of 140mm in this example.
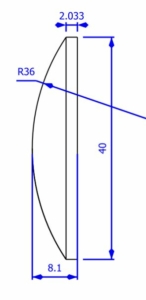
Illustration 2 : PCX lens
Illustration 2 : a plano-convex lens (PCX lens), with a flat surface on the right and a spherical convex surface on the left with a radius of curvature of 36mm in this example.
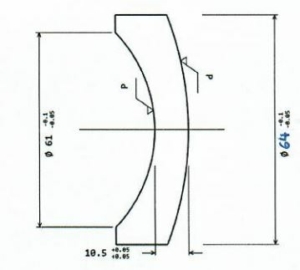
Illustration 3 : meniscus lens
Illustration 3: meniscus lens, thin lens with with a concave spherical surface on the left and a spherical concave surface of the on the right.
Illustration 4 : biconvex lens
Illustration 4: a biconvex lens with two surface of spherical convex surface with a radius of curvature of 80,5mm for both sides in this example.
Illustration 5 : biconcave lens
Illustration 5 : a biconcave lens with two spherical concave surfaces and a center thickness of 1,8mm in this example.
Remarks :
- It is also commun for some lenses to have one face non spherical and an other face spherical.
- In some publications an optical elements with both faces flat is called “flat lens”, we will not use this term and refer to these elements as optical windows as they are not shaped to converge of diverge the light.
How spherical lenses are made?
Normal process for manufacturing of a spherical lens is as below :
- Cut or mold a preform close to the shape of the lens

Lens preforms
- Grinding of the part to get the right shape
- Polishing of both optical surfaces on semi-automatic polishing device

Semi-automatic circular polishing machines
- Centering / edging of the lens to match the lens mechanical axis and optical axis. Lens centering is very important as bad centering will conduct to degradation of optical properties in the optical system after assembly.
- Cleaning of the lens with ultrasound cleaning machines

ultrasound cleaning bath
- Coating of the lens, in a coating device

Coating device
Which optical material can be used for spherical lens?
Most optical material can be used to manufacture a spherical lens, choice of material should be made according to below criteria :
- Refractive index (define how the light rays will react at the interface of air / lens)
- Abbe number (define the chromatic dispersion)
- Useful wavelength (UV, visible, IR)
- Point of fusion in case the lens is to be molded
- Availability / cost of material. Some material may be the exact match for your desing, but they may not be available or extremely expensive, therefore a close equivalent maybe considered.
- Usage conditions : for example under extreme condition extra hard material like sapphire may be chosen.
In case no specific constraint, we advise to design lens with N-BK7 ( Schott)/ HK9L (CDGM) optical glass, they are widely available and relatively cheap.
How much does a spherical lens cost?
Spherical lens can be found from a wide range from less than one USD to several thousand USD per lens. Below are the parameters that impact a lens price :
| Parameter | Impact on spherical lens cost |
|---|---|
| Raw material | Affordable materials : N-BK7/HK9L/B270/ Fused silica/Plastics, to more expensive materials : Sapphire, Germanium, Silicon, very specific optical material |
| Size | Very small (less than 5mm) and extra large lenses (more than 100mm) are more expensive to produce due to polishing difficulties related to the size. |
| Optical specifications | Polishing quality and surface quality have a very significant impact on the pricing of a spherical lens, and increase of specification can see a component price jumping to an other level |
| Order quantities | Polishing of spherical lenses can be done in parallel semi-automatic polishing machines, meaning that it wild take almost the same time and ressources to manufacture one or ten parts. |
| Optical coatings | Optical coatings is done per batch, one batch cost usually several hundreds of USD, therefore the more parts you can put in a device the cheaper the unit price will be, contact us for the optimum order quatity. |
If you are looking for a specific price for your project don’t hesitate to request for a free quotation :
Spherical lens focal length
The focal point of a spherical lens is the point on the optical axis at which an incident bundle of light rays will converge to focus.
The focal length, is the distance between the center of the lens and the focal point. The focal length is a positive value in case of converging lens, and negative in term of diverging lens.
According to the shape of the surfaces, a spherical lens can be diverging or converging.
The focal length formula (Gaussian formula) is :
1/u + 1/v = 1/f
Where :
u : is the distance of the object to the center of the lens
v: is the distance of the image to the center of the lens
f: is the focal length.
For example with an objet at the infinity, we will have 1/u that tend toward 0, so 1/v=1/f so v=f, the image will form at the focal length.
A spherical lens is defined by it’s optical power which is inverse equivalent to the focal length, meaning that the closer to the lens the focal point is the higher the power of the length.
P=1/f
Where P is the power of the lens and f the focal length.
The simulation of a spherical lens focal length can be done based on the refractive index of the material (Snell law), thickness of the lens and radius of curvature. As the calculus is little complicated we advise spherical lens users to use simulation software (like Zemax) to get a reliable value.
Spherical lens concentricity, a key specification
An optical lens usually have 2 types of tolerancing :
- optical tolerancing
- mechanical tolerancing
Concentricity is a direct link between both. Lens concentricity will define how close the optical center will be to the mechanical center, this is particularly important in an optical system involving several lenses assembled in the same mechanical barrel as concentricity error of each lens may adds up.